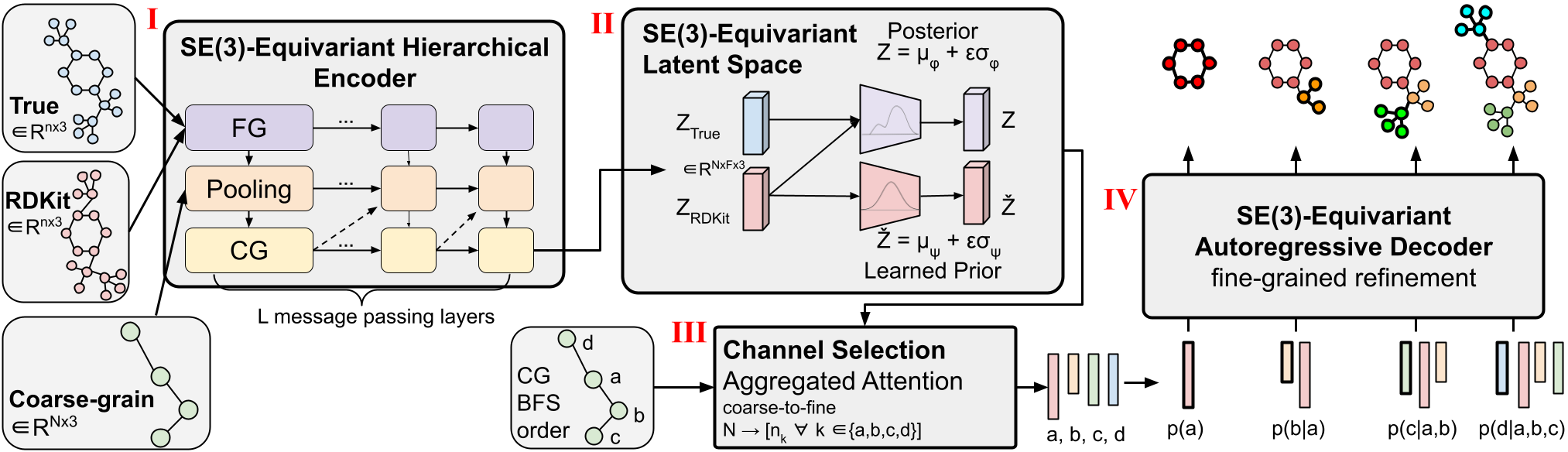
Determine 1: CoarseConf structure.
The era of molecular conformers is a basic activity in computational chemistry. The objective is to foretell secure low-energy 3D molecular constructions (referred to as conformers) given a 2D molecule. Correct molecular conformation is important for quite a lot of functions that depend on exact spatial and geometric qualities, together with drug discovery and protein docking.
We introduce CoarsenConf, a SE(3) equivariant hierarchical variational autoencoder (VAE) that swimming pools data from fine-grained atomic coordinates to coarse-grained subgraph-level representations to attain environment friendly autoregression Conformational isomer era.
background
Coarse-graining reduces the dimensionality of the issue, permitting conditional autoregressive era slightly than producing all coordinates independently as in earlier work. By immediately adjusting the 3D coordinates of beforehand generated subgraphs, our mannequin can higher generalize to chemically and spatially comparable subgraphs. This mimics the underlying molecular synthesis course of, the place small practical items come collectively to type massive drug-like molecules. Not like earlier strategies, CoarsenConf produces low-energy conformers and is ready to immediately mannequin atomic coordinates, distances, and torsion angles.
The CoarsenConf structure could be divided into the next parts:
(I) The encoder $q_phi(z| takes $mathcal{C}$ as enter (derived from $X$ and a predefined CG coverage), and outputs a variable-length equivariant CG illustration by means of equivariant message passing and level convolution.
(two) Equivariant MLP is utilized to be taught the imply and logarithmic variation of the posterior and prior distributions.
(three) The posterior (coaching) or prior (inference) is sampled and fed into the channel choice module, the place the eye layer is used to be taught the optimum path from CG to FG construction.
(4) Given an FG latent vector and an RDKit approximation, the decoder $p_theta(X |mathcal{R}, z)$ learns to get better low-energy FG constructions by means of autoregressive equivariant message matching. By optimizing the KL divergence of the latent distribution and the reconstruction error of the ensuing conformers, the complete mannequin could be skilled end-to-end.
MCG mission formalism
We formalize the duty of molecular conformation era (MCG) as modeling the conditional distribution $p(X|mathcal{R})$, the place $mathcal{R}$ is the approximate conformation generated by RDKit, $X $ is the optimum low-energy conformer. RDKit is a generally used chemical data library that makes use of cheap distance geometry-based algorithms adopted by cheap physics-based optimization to attain affordable conformational approximations.
Coarse grained
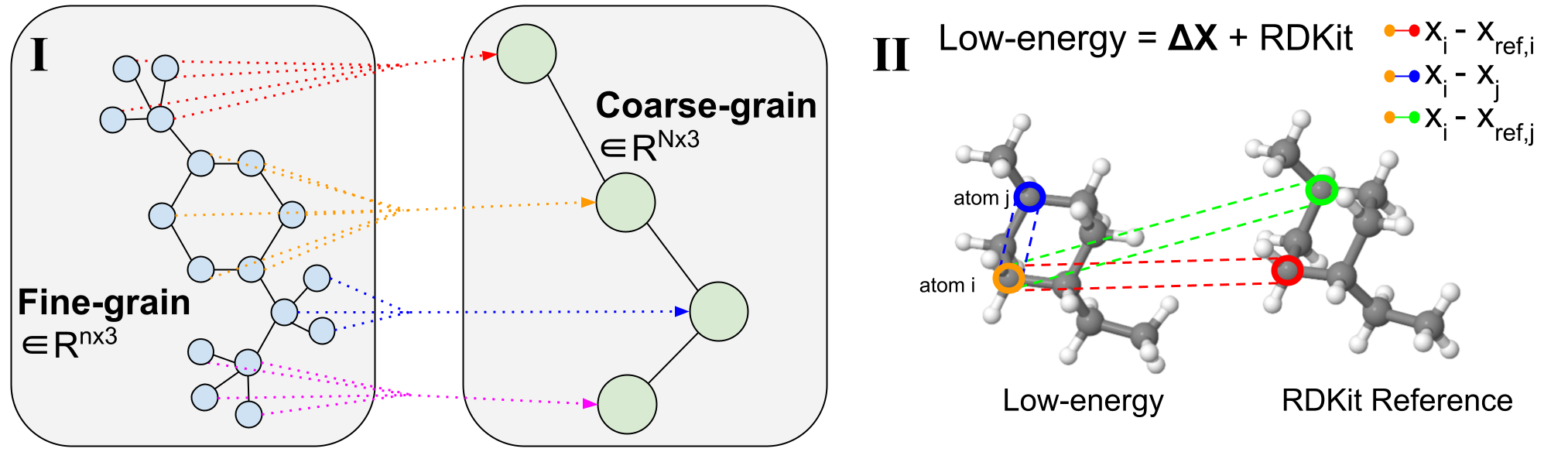
Determine 2: Coarse-grained course of.
(I) Instance of variable-length coarse-graining. High-quality-grained molecules cut up alongside rotatable bonds that outline the torsion angle. They’re then coarse-grained to scale back dimensionality and be taught subgraph-level latent distributions. (two) Visualization of 3D conformers. Spotlight particular atomic pairs to be used in decoder messaging operations.
Molecular coarse-graining simplifies molecular illustration by utilizing rule-based mapping to group fine-grained (FG) atoms within the authentic construction into particular person coarse-grained (CG) beads $mathcal{B}$ as proven in Determine 2 (i) . Coarse-graining has been extensively utilized in protein and molecule design, and comparable fragment-level or subgraph-level era has confirmed to be very helpful in numerous 2D molecular design duties. Breaking the era drawback into smaller components is an strategy that may be utilized to a number of 3D molecular duties and offers pure dimensionality discount to help working with massive, complicated techniques.
We word that in distinction to earlier work specializing in fixed-length CG methods (the place every molecule is represented at a set decision of $N$ CG beads), our strategy makes use of variable-length CG due to its flexibility and help The flexibility to make any tough decisions. granulation expertise. Which means a single CoarsenConf mannequin could be generalized to any coarse-grained decision, for the reason that enter molecules could be mapped to any variety of CG beads. In our case, the atoms consisting of every related element ensuing from slicing all rotatable bonds are coarsened into particular person beads. This selection within the CG course of implicitly forces the mannequin to know the torsion angle in addition to the atomic coordinates and interatomic distances. In our experiments, we use GEOM-QM9 and GEOM-DRUGS, which have a median of 11 atoms and three CG beads, and 44 atoms and 9 CG beads, respectively.
SE(3)-equal variances
A key side when working with 3D constructions is sustaining applicable isotropic properties. Three-dimensional molecules are equivariant in rotation and translation, or SE(3)-equivariant. We implement SE(3) equal variances within the encoder, decoder, and latent areas of the probabilistic mannequin CoarsenConf. Subsequently, $p(X | mathcal{R})$ stays unchanged for any rotational translation of the approximate conformer $mathcal{R}$. Moreover, if $mathcal{R}$ is rotated 90° clockwise, we count on the optimum $X$ to exhibit the identical rotation. See the complete article for an in-depth definition and dialogue of the strategy of sustaining equal variances.
focus consideration
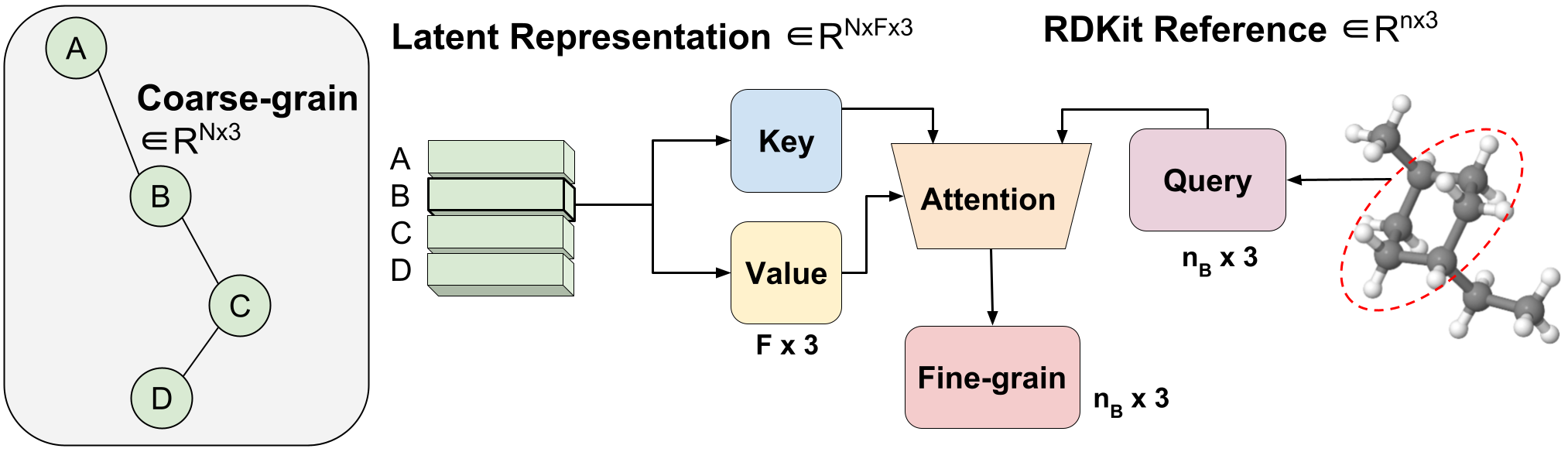
Determine 3: Variable-length coarse-to-fine inverse mapping by way of collective consideration.
We introduce a technique referred to as aggregated consideration to be taught an optimum variable-length mapping from latent CG representations to FG coordinates. It is a variable size operation as a result of a single molecule with $n$ atoms could be mapped to any variety of $N$ CG beads (every bead represented by a single latent vector). The latent vector of a single CG bead $Z_{B}$ $in R^{F instances 3}$ is used as the important thing and worth of a single-head consideration operation of embedding dimension 3 to match the x, y, z coordinates. The question vector is the subset of RDKit conformers comparable to bead $B$ $in R^{ n_{B} instances 3}$ , the place $n_B$ is of variable size as a result of we all know a priori that the corresponding What number of FG atoms go to a sure CG bead. Leveraging consideration, we successfully be taught an optimum combination of latent options for FG reconstruction. We name it aggregated consideration as a result of it aggregates 3D items of FG data to type our potential question. Aggregated consideration is chargeable for environment friendly transformation from potential CG representations to possible FG coordinates (Determine 1(III)).
Mannequin
CoarsenConf is a layered UAE with SE(3) equivariant encoders and decoders. The encoder operates on SE(3) invariant atomic options $h in R^{n instances D}$ and SE(3) equivariant atomic coordinates $x in R^{n instances 3}$. A single encoder layer consists of three modules: fine-grained, pooling, and coarse-grained. The entire equations for every module could be discovered within the full textual content. The encoder produces the ultimate equivariant CG tensor $Z in R^{N instances F instances 3}$, the place $N$ is the variety of beads and F is the user-defined potential measurement.
The decoder has two features. The primary is to rework the latent coarse illustration again into FG area by means of a course of we name channel choice, which exploits aggregated consideration. The second is autoregressive refinement of the fine-grained illustration to supply closing low-energy coordinates (Fig. 1 (IV)).
We spotlight that by means of the coarse-graining of torsion angle connections, our mannequin learns optimum torsion angles in an unsupervised method as a result of the conditional inputs to the decoder are misaligned. CoarsenConf ensures that every subsequent generated subgraph is accurately rotated to attain low coordinate and distance errors.
Experimental outcomes
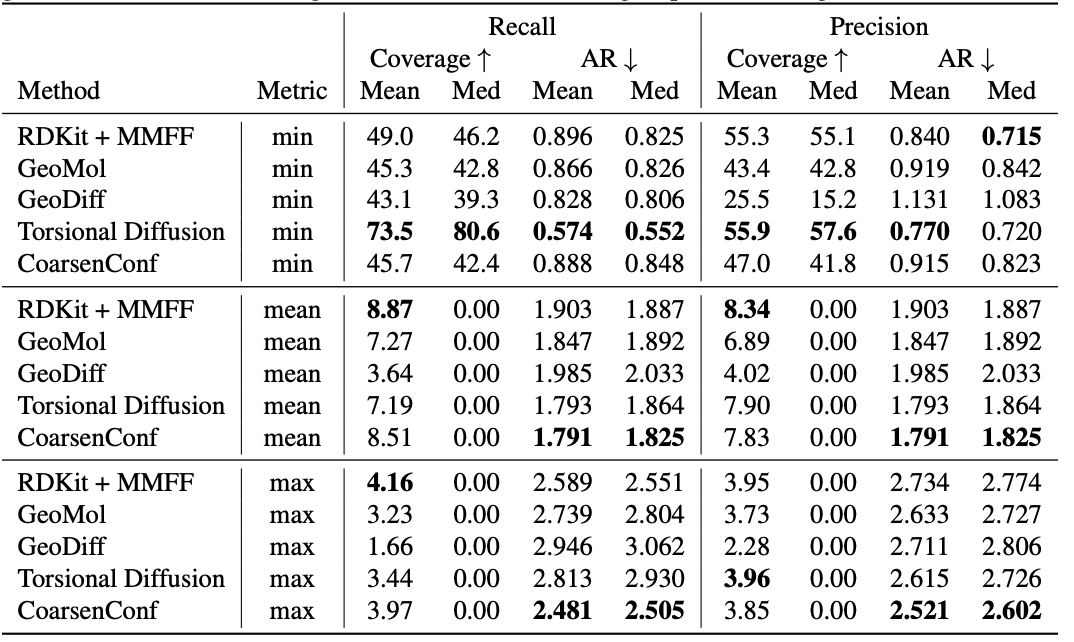
Desk 1: The standard of the ensemble of conformers produced by the GEOM-DRUGS check set ($delta=0.75Å$), expressed as protection (%) and common RMSD ($Å$). CoarsenConf (5 epochs) is restricted to 7.3% of the info utilized by Torsional Diffusion (250 epochs) to exemplify low-computation and data-limited mechanisms.
Common error (AR) is a key measure of the common RMSD of molecules generated from an applicable check set. Protection measures the share of molecules that may be produced inside a particular error threshold ($delta$). We introduce imply and most metrics to raised consider strong era and keep away from sampling bias of minimal metrics. We emphasize that minimal metrics yield intangible outcomes as a result of there is no such thing as a strategy to know which of the 2L conformers produced by a single molecule is one of the best until the optimum conformer is understood a priori. Desk 1 reveals that CoarsenConf produces the bottom common and worst-case errors throughout the complete check set of drug molecules. We additional present that RDKit with low cost physics-based optimization (MMFF) achieves higher protection than most deep learning-based strategies. For a proper definition of the indicator and additional dialogue, please see the complete textual content linked under.
For extra particulars on CoarsenConf, learn the paper on arXiv.
bibliographic textual content
If CoarsenConf impressed your work, please think about citing it within the following methods:
@article{reidenbach2023coarsenconf,
title={CoarsenConf: Equivariant Coarsening with Aggregated Consideration for Molecular Conformer Era},
creator={Danny Reidenbach and Aditi S. Krishnapriyan},
journal={arXiv preprint arXiv:2306.14852},
yr={2023},
}



